무한은 어떻게 수학의 악마에서 천사가 되었나? 게오르그 칸토어의 집합론 이야기
무한은 어떻게 수학의 악마에서 천사가 되었나? 게오르그 칸토어의 집합론 이야기
안녕하세요, 수학 친구들! 오늘은 '수학 사상의 결정적 전환점' 시리즈에서 무한의 이야기를 해볼게요. 무한이란 게 뭐냐고요? 끝없이 이어지는 길처럼, 숫자가 영원히 계속되는 개념이죠. 옛날 수학자들은 이걸 '악마'처럼 피했어요. 왜냐면 머리를 아프게 하고, 모순을 만들어냈으니까요. 그런데 19세기 독일 수학자 게오르그 칸토어가 나타나 무한을 '천사'로 바꿔놓았어요. 마치 동화 속 마법사처럼, 집합론이라는 마법 지팡이로요. 수학을 모르는 친구에게 이야기하듯, 복잡한 건 빼고 재미있는 에피소드와 비유로 풀어볼게요. 이 이야기가 끝나면 무한이 왜 AI나 빅데이터의 친구가 됐는지 알게 될 거예요.
무한의 어두운 시대: 악마로 불리던 시절
상상해 보세요, 고대 그리스 시대. 철학자 제논이 "아킬레스가 거북이를 절대 따라잡을 수 없다"는 역설을 던졌어요. 왜? 아킬레스가 거북이 위치에 도달할 때마다 거북이는 조금 더 앞으로 가 있으니까. 이건 무한히 작은 거리를 무한히 나누는 문제예요. 마치 끝없는 계단을 오르는 기분이죠. 아리스토텔레스는 무한을 '잠재적'으로만 인정했어요. 실제로 무한은 존재하지 않고, 그냥 '계속될 수 있다'고요. 중세에는 신학자들이 무한을 신의 영역으로 치부하며 피했어요. 무한을 다루면 모순이 생겨 수학의 기반이 흔들릴까 봐 두려웠죠.
19세기 초까지도 무한은 '악마'였어요. 칼슘 같은 수학자들이 미적분에서 무한을 쓰긴 했지만, 엄격하게 정의하지 않았어요. 마치 안개 낀 숲처럼, 무한은 위험한 미지의 영역이었어요. 그런데 칸토어가 이 숲에 불을 켜기로 결심했어요.
칸토어의 등장: 무한을 길들이는 모험가
1845년 러시아 상트페테르부르크에서 태어난 칸토어는 음악가 집안 출신이었어요. 아버지는 바이올린 연주자, 어머니는 피아니스트. 칸토어도 음악 재능이 있었지만, 숫자의 세계에 빠졌어요. 베를린 대학에서 공부하며, 숫자의 패턴을 탐험하기 시작했죠. 그의 첫 모험은 '무한 집합'을 다루는 거였어요.
집합이란? 그냥 물건들의 모임이에요. 예를 들어, 사과 바구니나 친구 목록처럼요. 칸토어는 이 집합으로 무한을 설명했어요. 자연수 집합 {1,2,3,...}은 무한이죠. 짝수 집합 {2,4,6,...}도 무한이에요. 상식적으로 자연수가 더 많아 보이지만, 칸토어는 "둘 다 같은 크기의 무한"이라고 했어요. 어떻게? 각 자연수에 짝수를 매칭하면 끝없이 이어지니까요. 1-2, 2-4, 3-6... 마치 무한한 짝짓기 춤처럼요.
더 놀라운 건, 실수 집합(소수점 있는 숫자들)은 자연수보다 '더 큰' 무한이라는 거예요. 칸토어는 대각선 논법으로 증명했어요. 실수 목록을 만들면, 대각선으로 숫자를 바꿔 새로운 실수를 만들 수 있어요. 이건 목록에 없는 숫자라, 실수는 셀 수 없이 많아요. 마치 바다 모래알처럼, 자연수 무한은 강물처럼 셀 수 있지만 실수 무한은 바다처럼 셀 수 없어요.
이 아이디어는 수학계를 뒤집었어요. 동료들은 "미쳤다!"라고 비난했죠. 레오폴드 크로네커는 "신만이 무한을 안다"고 공격했어요. 칸토어는 우울증으로 고생하며 병원에 입원하기도 했지만, 포기하지 않았어요. 그의 집합론은 무한을 '악마'에서 '천사'로 바꿨어요. 이제 무한은 수학의 도구가 됐죠.
칸토어의 칸토어 집합: 무한의 재미있는 퍼즐
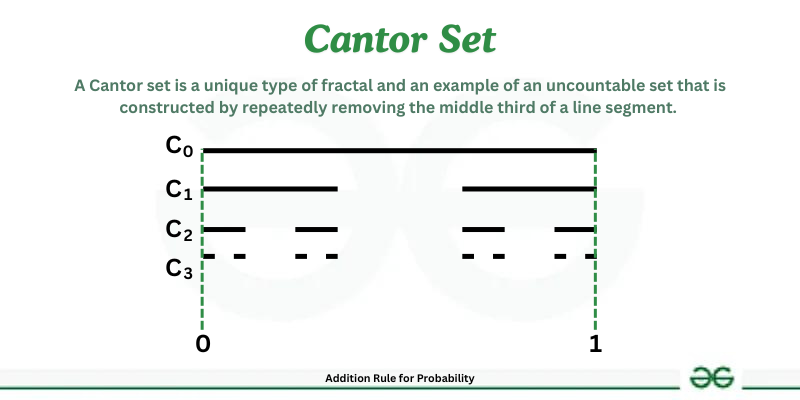
칸토어의 재미있는 발견 중 하나는 '칸토어 집합'이에요. 0부터 1까지 선분에서 시작해, 중간 1/3을 지우고, 남은 부분의 중간 1/3을 또 지우는 거예요. 이걸 무한히 반복하면? 길이는 0이 되지만, 점은 무한히 많아요. 마치 먼지처럼, 보이지도 않는데 무한한 점들! 이건 프랙탈의 원조예요. 상상해 보세요, 끝없는 분할로 만들어진 마법의 먼지. 이 퍼즐은 무한이 얼마나 이상한지 보여주죠.
무한의 유산: AI와 빅데이터 시대의 천사
칸토어의 집합론은 오늘날 어떻게 쓰일까요? AI에서 무한 집합은 데이터 구조의 기반이에요. 빅데이터 분석에서 무한한 가능성을 다루죠. 예를 들어, 메타버스에서 가상 세계는 무한한 좌표로 만들어져요. 구글 검색 알고리즘이나 챗GPT 같은 AI는 무한한 데이터셋을 처리할 때 칸토어의 아이디어를 빌려요. 최근 AI 붐에서 '무한 생성' 모델이 뜨고 있죠. 무한을 이해하면, 빅데이터의 '크기'를 비교할 수 있어요. 자연수처럼 셀 수 있는 데이터 vs. 실수처럼 셀 수 없는 빅데이터.
칸토어는 1918년 세상을 떠났지만, 그의 이야기는 계속돼요. 무한은 이제 수학의 천사예요. 이 시리즈에서 다음은 힐베르트의 무한 호텔 이야기로 갈까요? 재미있게 느껴지시나요?
어떤 무한 이야기가 궁금하세요? 댓글로 알려주세요! 함께 퍼즐 풀며 수학의 모험을 즐겨요.