비유클리드 기하학의 등장: 평행선 공리를 깨뜨린 수학의 대혁명
비유클리드 기하학의 등장: 평행선 공리를 깨뜨린 수학의 대혁명
안녕하세요, 수학 친구들! 오늘은 "수학 사상의 결정적 전환점" 시리즈의 첫 번째 이야기로, 비유클리드 기하학의 탄생을 들려드릴게요. 상상해 보세요. 2000년 넘게 누구도 의심하지 않았던 '평행선은 영원히 만나지 않는다'는 규칙이 깨지는 순간. 마치 지구가 둥글다는 사실을 처음 알았을 때처럼 세상이 뒤집히는 기분 아닐까요? 이 포스트에서는 수학을 잘 모르는 친구에게 이야기하듯, 복잡한 수식 없이 재미있는 비유와 스토리로 풀어갈게요. 함께 수학의 모험을 떠나 보아요!
유클리드의 완벽한 세계: 평행선 공리의 탄생
먼저, 고대 그리스의 수학자 유클리드를 만나보죠. 기원전 300년경, 그는 《기하학 원론》이라는 책으로 세상을 놀라게 했어요. 이 책은 직선, 원, 삼각형 같은 기본 도형을 다루며, 다섯 가지 공리를 기반으로 해요. 그중 다섯 번째가 바로 '평행선 공리'예요. "한 직선 밖의 한 점을 지나면서 그 직선과 평행한 직선은 단 하나뿐이다."
이걸 비유로 설명하면, 철로를 생각해 보세요. 기차 선로처럼 두 선이 평행하면 영원히 만나지 않죠? 유클리드는 이 규칙으로 평평한 종이 위 세계를 완벽하게 설명했어요. 학교에서 배우는 기하학이 바로 이거예요. 수천 년 동안 건축가, 엔지니어, 과학자들이 이 공리를 의심 없이 썼어요. 마치 지구가 평평하다고 믿던 시절처럼요!
하지만 여기서 재미있는 스토리가 시작돼요. 수학자들은 이 다섯 번째 공리가 다른 네 공리만큼 '자명'하지 않다고 느꼈어요. "이걸 증명할 수 없을까?" 하며 수백 년 동안 머리를 쥐어짰죠. 만약 증명 못 하면? 수학의 기초가 흔들릴 수 있어요.
공리를 깨뜨린 용감한 수학자들: 가우스, 보야이, 로바체프스키
19세기 초, 세 명의 천재가 이 미스터리를 풀었어요. 먼저 독일의 카를 프리드리히 가우스. 그는 '수학의 왕자'로 불릴 만큼 똑똑했지만, 이 아이디어를 공개하지 않았어요. 왜냐면 기존 수학계가 받아들일 준비가 안 됐다고 생각했거든요. 마치 혁명적인 아이디어를 숨기는 과학자처럼요.
그리고 헝가리의 야노스 보야이. 젊은 나이에 아버지에게 편지를 보냈어요: "나는 아무것도 없는 데서 새로운 우주를 창조했다!" 보야이는 평행선 공리를 부정하면 새로운 기하학이 나온다는 걸 발견했죠. 마지막으로 러시아의 니콜라이 로바체프스키. 그는 독립적으로 같은 결론에 도달해 논문을 발표했어요.
이들의 발견은 '비유클리드 기하학'이에요. 평행선 공리를 바꾸면 세상이 어떻게 달라질까요? 두 가지 유형으로 나눠 보죠.
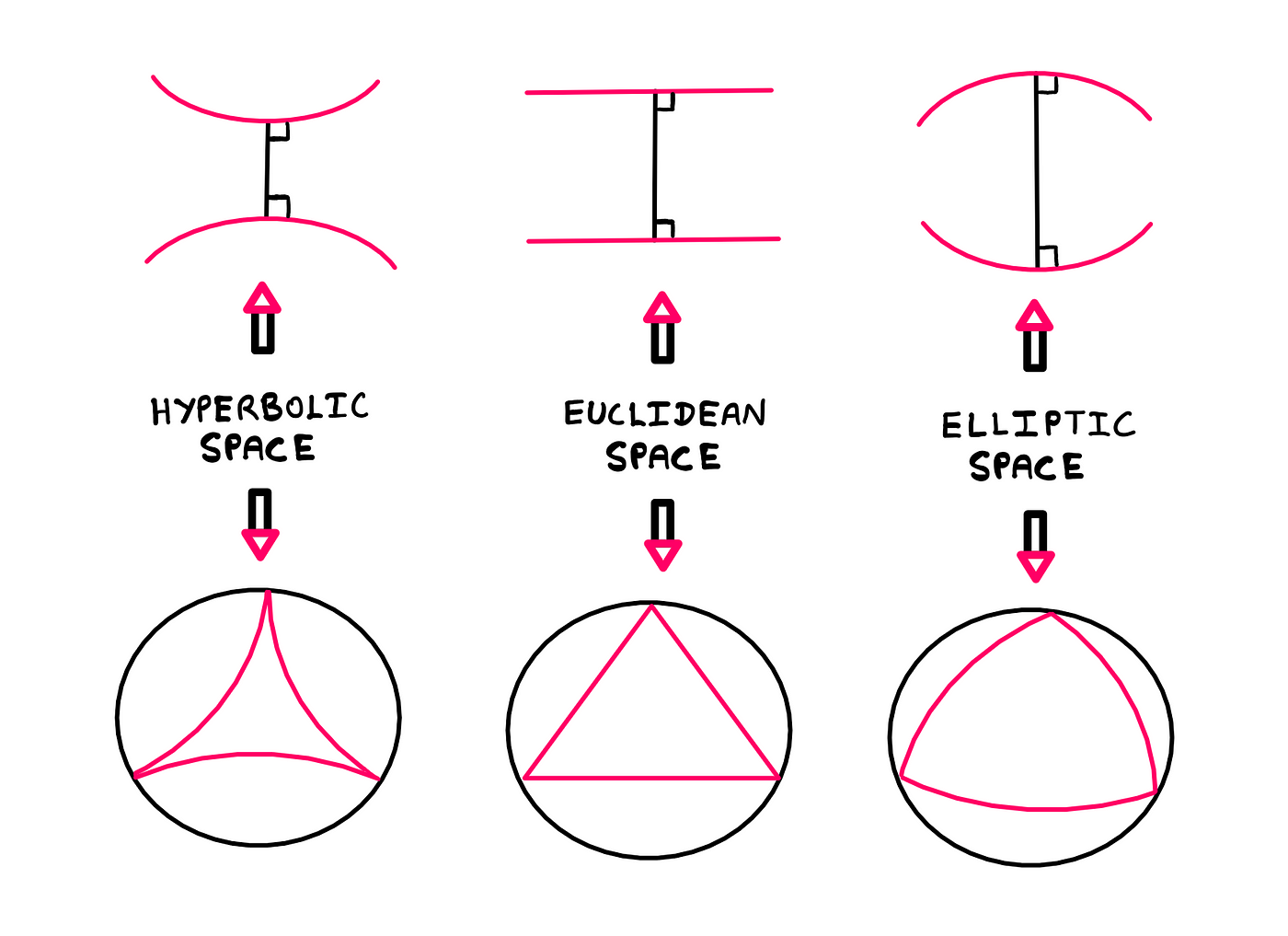
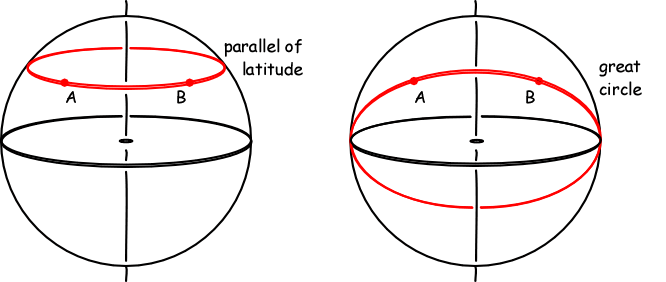
- 타원 기하학 (구면 기하학): 지구 표면을 상상해 보세요. 적도처럼 평행한 선이 없어요. 모든 선(대권)은 결국 만나죠. 예를 들어, 경도선들은 북극과 남극에서 만납니다. 삼각형 내각 합이 180도 넘어요. 마치 풍선 위에서 그린 도형처럼요!
- 쌍곡 기하학: 안장 모양의 표면을 생각해 보세요. 한 점을 지나 평행선이 여러 개 생겨요. 삼각형 내각 합이 180도 미만이에요. 상상하기 어렵죠? 잎사귀나 산호초처럼 구불구불한 모양이에요.
이 비유로 보니, 유클리드 기하학은 평평한 바닥, 비유클리드는 굽은 세계예요. 마치 평면 TV에서 3D 영화로 넘어가는 느낌!
비유클리드 기하학이 바꾼 세상: 물리학과 현대 기술
이 발견은 수학만 바꾼 게 아니에요. 알베르트 아인슈타인의 일반상대성 이론에서 빛을 발했죠. 우주는 평평하지 않고, 중력으로 굽어요. 블랙홀 근처 공간은 쌍곡 기하학처럼 휘어요. 마치 우주가 거대한 안장 모양인 거예요!
최신 트렌드와 연결해 보죠. AI와 메타버스에서 비유클리드 기하학은 필수예요. 가상 현실(VR) 게임에서 공간을 왜곡하면, 무한한 세계를 만들 수 있어요. 예를 들어, 마인크래프트 같은 게임에서 비유클리드 맵을 만들면, 방이 실제보다 커 보이죠. 빅데이터 분석에서도 곡면상의 데이터 처리를 위해 써요. AI가 지구상 교통 흐름을 예측할 때, 지구의 구면을 고려하잖아요?
상상해 보세요. 메타버스에서 친구와 산책하는데, 길이 휘어져 예상치 못한 곳으로 가는 거예요. 이게 비유클리드의 마법이에요!
마무리: 수학의 새로운 지평과 당신의 생각
비유클리드 기하학은 "절대 진리는 없다"는 교훈을 줘요. 유클리드의 세계가 유일한 게 아니라는 깨달음이죠.